554. Вписанная окружность
Окружность
называется вписанной в многоугольник, если она имеет точку касания с каждой его
стороной.
Определите,
можно ли в заданный выпуклый многоугольник вписать окружность, и, если это
можно сделать, то вычислите координаты её центра и радиус.
Вход. Первая строка содержит количество
вершин многоугольника n (3 ≤ n ≤ 8). Следующие n строк содержат координаты вершин
многоугольника в порядке обхода против часовой стрелки, каждая строка содержит
два целых числа: xi и yi, значения которых не
превосходят 1000 по абсолютной величине.
Выход. Если
окружность, вписанная в заданный многоугольник, существует, то вывести в первой
строке слово YES, иначе вывести слово NO. В случае положительного ответа
выведите во второй строке координаты центра окружности и её радиус. Ответ
выводите с точностью 10-6.
|
Пример входа |
Пример выхода |
|
4 0 0 1 0 1 1 0 1 |
YES 0.500000
0.500000 0.500000 |
РЕШЕНИЕ
вычислительная
геометрия
Анализ алгоритма
Построим
биссектрисы двух соседних углов многоугольника и найдем точку (xc, yc) их пересечения. Если в многоугольник можно вписать
окружность, то эта точка будет ее центром. Вычисляем радиус окружности r. Находим расстояния от (xc, yc) до всех сторон многоугольника. Если все они равны r, то в многоугольник можно вписать
окружность. Иначе нельзя.
Пусть a1 x + b1 y + c1 = 0 и a2 x + b2 y + c2
= 0 – уравнения сторон угла. Тогда уравнение биссектрисы угла (как
геометрическое множество точек, равноудаленных от сторон угла) имеет вид:
 =
= 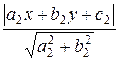
Реализация алгоритма
Координаты точек
(xi, yi) многоугольника храним в (x[i], y[i]).
#define MAX 10
#define EPS 1e-7
int
x[MAX], y[MAX];
Функция Bisect находит уравнение биссектрисы ax + by
+ c = 0 угла многоугольника при
вершине (xn, yn) (то есть угол между
сторонами (xn-1,
yn-1) – (xn, yn) и (xn, yn) – (xn+1,
yn+1) ).
void
Bisect(int n, double
&a, double &b, double
&c)
{
Переименуем точки.
double x0 =
x[n-1], y0 = y[n-1];
double x1 =
x[n], y1 = y[n];
double x2 =
x[n+1], y2 = y[n+1];

Уравнение прямой AB:  =
=  или
или
(y1 – y0)x + (x0
– x1)y + x1 y0 – x0 y1
= a1 x + b1 y + c1
= 0
Уравнение прямой BC:  =
=  или
или
(y2 – y1)x + (x1
– x2)y + x2 y1 – x1 y2
= a2 x + b2 y + c2
= 0
double a1 =
y1 - y0, a2 = y2 - y1;
double b1 =
x0 - x1, b2 = x1 - x2;
double c1 =
x1*y0 - x0*y1;
double c2 =
x2*y1 - x1*y2;
Если a1 x + b1 y + c1 = 0 и a2 x + b2 y + c2
= 0 – уравнения сторон угла, то уравнение биссектрисы угла (как геометрическое
множество точек, равноудаленных от сторон угла) имеет вид:
 =
= 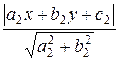
Опустим модуль, обозначим d1 = ![]() , d2 =
, d2 = ![]() и перепишем уравнение
в виде:
и перепишем уравнение
в виде:
![]() =
= ![]() ,
,
![]() =
= ![]() = 0
= 0
double d1 =
sqrt(a1*a1 + b1*b1);
double d2 =
sqrt(a2*a2 + b2*b2);
a = a1 * d2 - a2 * d1;
b = b1 * d2 - b2 * d1;
c = c1 * d2 - c2 * d1;
}
Решение системы
линейных уравнений методом Крамера. Поскольку две смежные биссектрисы всегда
пересекаются, не будем отслеживать случай, когда система уравнений не имеет
(имеет бесконечно много) решений.
void
kramer(double a1,double
b1, double c1,
double a2, double
b2, double c2, double
&x, double &y)
{
double d = a1
* b2 - a2 * b1;
double dx =
c1 * b2 - c2 * b1;
double dy =
a1 * c2 - a2 * c1;
x = dx/d; y = dy/d;
}
Вычисление расстояния
от точки (x, y) до прямой ax + by + c
= 0, равного
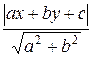
double dist(double a, double b, double c, double x, double y)
{
return
fabs(a*x+b*y+c) / sqrt(a*a + b*b);
}
Основная часть
программы. Читаем входные данные.
scanf("%d",&n);
for(i
= 0; i < n; i++)
scanf("%d
%d",&x[i],&y[i]);
x[n]
= x[0]; y[n] = y[0];
Находим уравнения биссектрис
первого и второго угла.
Bisect(1,a1,b1,c1);
Bisect(2,a2,b2,c2);
Методом Крамера находим точку
пересечения биссектрис (xc, yc). Вычисляем радиус r искомой окружности как расстояние от
центра (xc, yc) до прямой (x0, y0) – (x1,
y1) (существование самой
окружности проверим ниже).
kramer(a1,b1,-c1,a2,b2,-c2,xc,yc);
r
= dist(y[1] - y[0],x[0] - x[1],x[1]*y[0] - x[0]*y[1],xc,yc);
Вычисляем расстояния от точки (xc, yc) до всех сторон
многоугольника. Если все они равны r,
то вписанная в многоугольник окружность существует.
for(i
= 1; i < n; i++)
{
d = dist(y[i+1] - y[i], x[i] -
x[i+1],x[i+1]*y[i] - x[i]*y[i+1],xc,yc);
if (fabs(d -
r) > EPS)
{
printf("NO\n");
return 0;
}
}
Выводим центр и
радиус искомой вписанной окружности.
printf("YES\n");
printf("%.6lf %.6lf %.6lf\n",xc,yc,r);